高考数学小题狂做·基础篇
P2 Q14
非空集合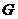 关于运算“
关于运算“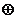 ”满足:①对于任意
”满足:①对于任意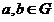 ,都有
,都有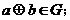 ②存在
②存在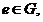 使对于一切
使对于一切 ,都有
,都有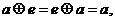 则称
则称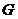 关于运算“
关于运算“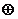 ”为融洽集.现有下列集合运算:
”为融洽集.现有下列集合运算:
(1)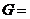 {非负整数},“
{非负整数},“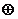 ”为整数的加法;
”为整数的加法;
(2)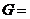 {偶数},“
{偶数},“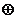 ”为整数的乘法;
”为整数的乘法;
(3)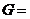 {平面向量},“
{平面向量},“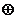 ”为平面向量的加法;
”为平面向量的加法;
(4)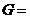 {二次三项式},“
{二次三项式},“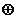 ”为多项式的加法.
”为多项式的加法.
其中关于运算“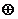 ”为融洽集的有________(填序号).
”为融洽集的有________(填序号).
考点说明:集合中的新定义问题
问题解答:本题是一道关于集合的新定义问题,主要难度在于理解题目中提出的新概念:题中叙述的两个性质,其一是指运算对集合内元素“封闭”,即任意两个集合内的元素经过运算后得到的结果仍在属于这个集合;其二是对于该运算集合中存在“零元”,即任意元素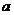 与该“零元”运算后得到的结果仍然是
与该“零元”运算后得到的结果仍然是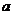 本身(引号中的概念是高等代数中的概念,可以不用在意)
本身(引号中的概念是高等代数中的概念,可以不用在意)
符合以上两个要素的集合与运算的例子可以是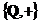 ,即有理数集关于加法满足以上两个性质,其中性质(2)中的
,即有理数集关于加法满足以上两个性质,其中性质(2)中的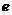 为0。
为0。

微信小程序
微信扫一扫体验

微信公众账号
微信扫一扫加关注
评论 返回
顶部

发表评论 取消回复